Digital Craftsmanship
Craftmanship and digital technology in surface design
Before the era of computer-aided design, like everyone else, industrial designers also had solutions different from today's. For example, when creating car bodies, they worked with overlaid transparent cross-section layers, clay models, the experience of sheet metal pressers, and similar tools. The digital age offers a range of new possibilities while rendering others unnecessary or costly. No one lays transparent layers of cross-sections on top of each other anymore to infer the behavior of a surface. Instead, a virtual model of the concept can be created. Clay modelers have also exchanged their knives and chisels for software because models are now carved by CNC machines. This is more efficient. The expertise of the craftsman is still necessary, but machines, when employed, carry out the physical part of their work more efficiently. In fact, the machine extends the hand of the craftsman. Thus, manual dexterity is digitized. Just as the clay modeler shaped clay in the heyday of car design, now the surface modeler shapes virtual surfaces, which are then realized by machines. This is a kind of digital sculpture. To achieve the desired result, two conditions must be met:
It must work!
It must be beautiful!
For it to work, every tiny detail must be devised and digitally determined. All of this must be done in a way that the result is appealing. This depends not only on the skill of the designer but also on the software they use. Some programs allow for quickly creating complex but less accurate shapes, which is useful in the early stages of design. Other programs focus on manufacturing accuracy, which is also understandable. For the latter purpose, CAD systems are used. With these, manufacturable designs can be created, but it is difficult to create truly beautiful surfaces with them. Let's take an example, a hood that must fit the shape of a car. It must precisely continue the curves running on the car body and reflect light, all while fitting precisely with the surrounding components, considering even the oscillation caused by closing. Therefore, the geometry must be fine-tuned simultaneously for aesthetic and technical reasons. The answer of the digital age to this demand is the A-Class surface modeling, based on Bezier curve, and the Bezier surface created from it.

1. Bezier-curve
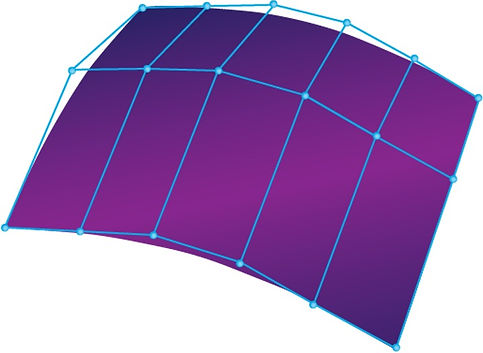
2. Bezier-surface
This curve and surface can be changed by moving their corresponding control points. The simplest curve is the linear Bezier curve, which is a straight line with a control point at each end. If a curve has three or more control points, and they do not lie on a straight line, then the curve is at least twice continuously differentiable at every point, meaning it is second-degree continuous (G2). This means that there cannot be abrupt changes in the segment between the two endpoints of the curve, only gradual transitions. It is this property that makes the Bezier curve so special. This means that the complex geometry built from connecting Bezier surfaces can only be discontinuous along the surface boundaries, and therefore, faulty. The surface modeler manipulates these small surface pieces to find the arrangement where the transition along the surface boundaries is also second-degree (G2) continuous, while not deviating significantly from the original design concept.
As an example, let's examine a four-control-point curve projected onto a convex surface from top view. The new curve is influenced by the target surface, so the original curve's degree is not sufficient for accurately describing the result. With only four control points, it's impossible to describe a curve lying on a surface with, say, six control points. For manageability reasons, it's not advisable to raise the degree above 7, but to refine the result, increasing the number of curves along with their subdivision can be employed. However, having more curves also means more connecting points, where, as we've seen, continuity becomes questionable. These points often require manual adjustment later. If continuity is not important because we're working with internal, unseen curves or surfaces, then this process can be automated. This is parametric modeling, which is the solution of CAD systems for fast and flexible handling of 3D models. These typically use NURBS curves (multi-span curve), which can easily handle complex geometry. While they can be clearly broken down into a series of Bezier curves (single-span curve), they do not guarantee G2 continuity between them. This means that the degree of convexity of a NURBS surface can vary abruptly between its edges, which is clearly visible in the reflections of light on it. Therefore, if continuity is an important factor, NURBS curves and surfaces, and thus classical CAD systems, are not suitable for such work. They simply weren't designed for it. To create A-Class quality surfaces, we need software capable of individually handling Bezier curves and surfaces.
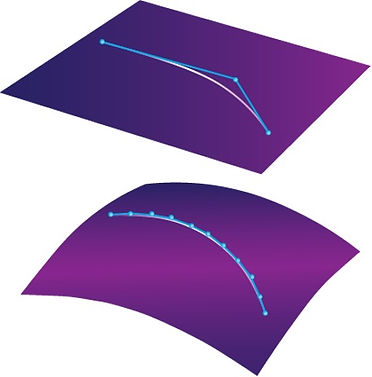
3. Projecting a Bezier curve onto a surface with software that can work with Bezier curves
Result: two Bezier curves (single-span curves). They can be modified and reconnected if necessary (G2).
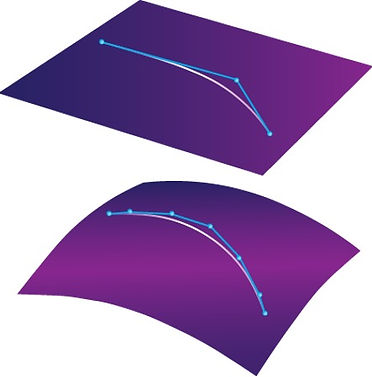
4. Projecting a Bezier curve onto a surface with software that does not support Bezier curves.
Result: a NURBS curve with an internal connection point in the middle (multi-span curve). Due to its complexity, it's cumbersome to modify. To fix any potential internal error, it would need to be segmented.
A defining feature of A-Class modeling is that changing one value doesn't update the entire model, unlike a well-structured parametric model. Each surface patch must be reconnected individually (there's no history tree). That's why there's a need to minimize the number of surface patches and control points, as modifying them entails more work. It depends on the skill of the modeler to shape the structure of the surfaces. There's no universal recipe, only proven practices. Each situation is slightly different, so aesthetic sense and creativity are also necessary for successful work.
Based on all this, A-Class modeling is a technique for creating surfaces where technology and art assist each other. This tool enables the modeler to sensually and precisely shape various products, much like a craftsman shapes the material in their hands. A-Class modeling thus represents the close collaboration between artistic inclination and engineering precision, opening the way to products that are not only technically high-quality but also aesthetically sophisticated and attractive.
In the hands of the surface modeler are a few tools that help understand the behavior of a surface. Among these, the following two are perhaps the most important:
Curvature analysis:
This tool helps examine the curve or surface of multiple interconnected curves. It places stripes on them in such a way that each stripe indicates the change in steepness of the given curve. The longer a stripe, the faster the direction of the tangent changes at that specific point on the curve compared to neighboring points. Our curves will have a smooth arc if the stripes change uniformly.

5. The curvature analysis is continuous, with no breaks, ensuring that the hood's curve changes harmoniously.
Zebra (highlight) analysis:
This tool simulates how light falling on surfaces is reflected. Natural light typically comes from above, so the direction of illumination is generally vertical. To obtain useful information, it is advisable to project multiple parallel light stripes onto the surface. This creates a characteristic zebra graphic on the surfaces, defined by the light and dark lines reflected on the surface. Where the curvature of the stripes is not harmonious or appears uncertain, the surface modeler still has work to do.

6. Reflection of natural light

7. Zebra analysis from the Z direction.

8. The Zebra analysis shows how natural light will reflect on the finished product.
If you want to learn more about our approach to create beautifully crafted products, please contact us about our training program, which begins in early 2025.
We are also working on a downloadable booklet that will soon be available for purchase on our website.
